Diagramme De Distribution Normale Ou Courbe Gaussienne De Bell Sur Le Tableau Illustration de
Figure 20 Courbes de Gauss en fonction de σ (même moyenne)
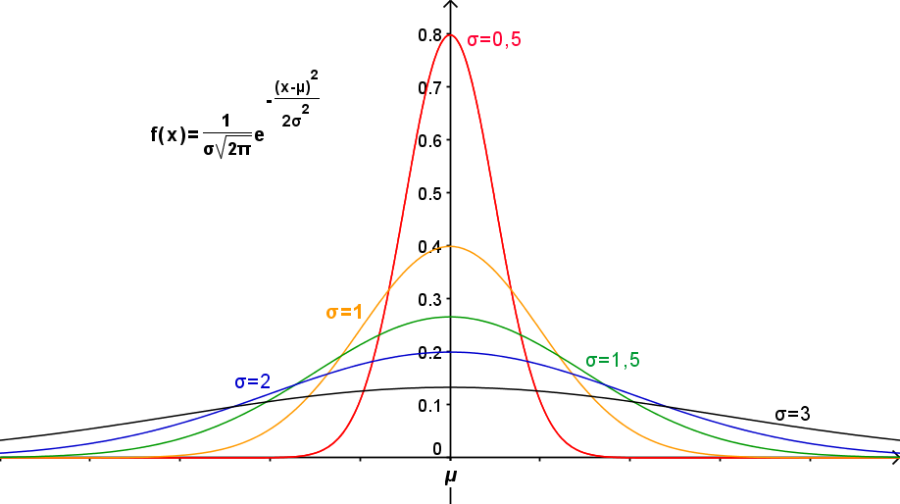
Notes 1 Gauss (1777-1855) est un mathématicien, astronome et physicien allemand. Surnommé "le prince des mathématiciens", il est considéré comme l'un des plus grands mathématiciens de tous les temps. 2 Laplace (1749-1827) est un mathématicien, astronome et physicien français. Laplace est l'un des principaux scientifiques de la période napoléonienne ; il a apporté des contributions.
distribución de Gauss. distribución normal estándar. Curva gráfica de campana de Gauss. concepto
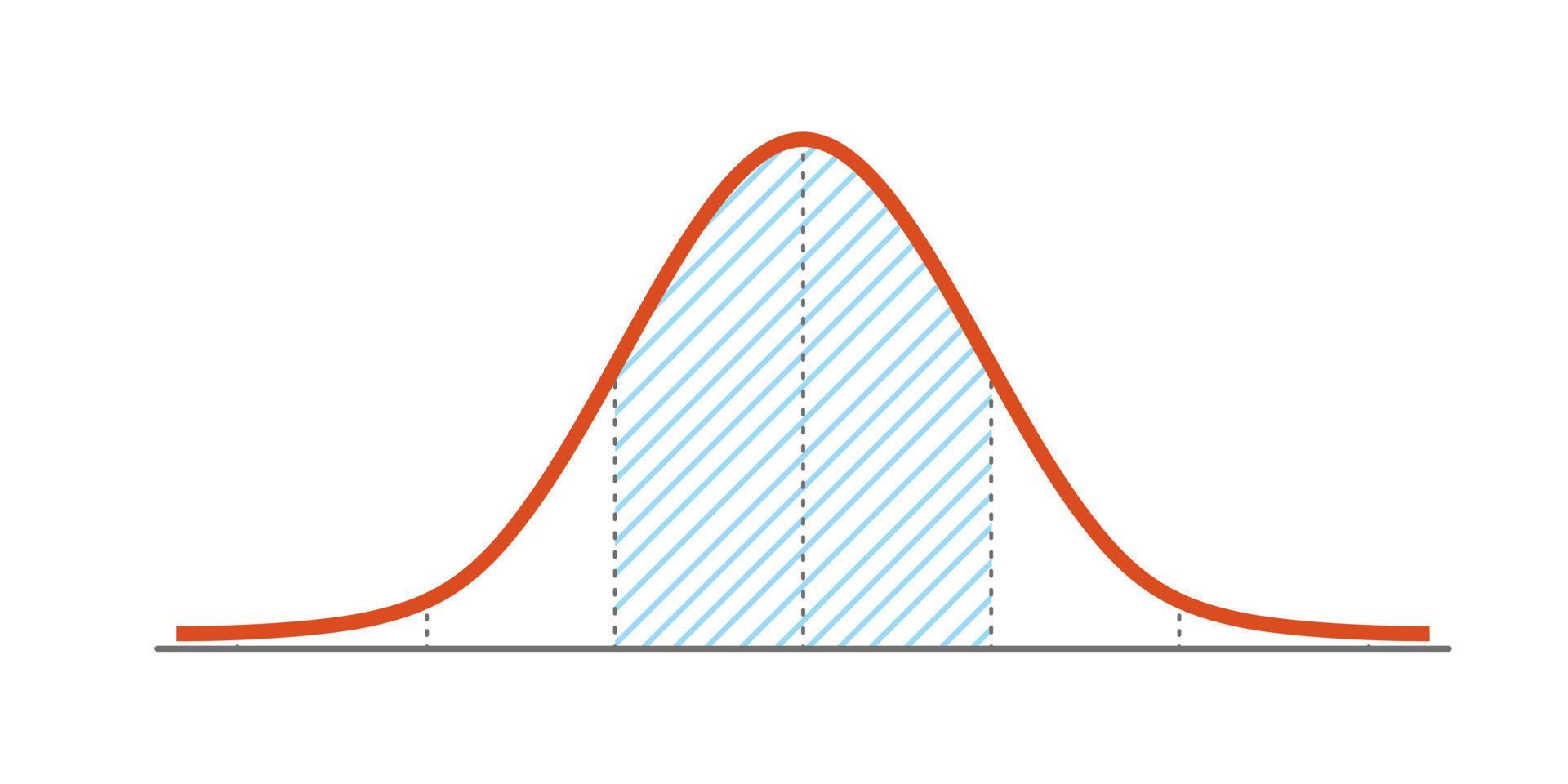
chapitre 5: La loi normale. 1. Loi normale ou de Gauss. Supposons que nous tirions des échantillons aléatoires d'une population dont la taille moyenne est de 170 cm , avec un écart type de 10 cm . Traçons l'histogramme de la taille, avec des classes de 5 cm de large, pour des échantillons de plus en plus grands.
Gaussian distribution, standard normal distribution, bell curve Digital Art by Peter Hermes
Courbe de Gauss. Gaussian Distribution. La courbe de Gauss permet de représenter visuellement la distribution d'une série et en particulier la densité de mesures d'une série. Elle utilise les deux calculs de l'espérance et de l'écart-type de la série. Pour un échantillon important, il est généralement constatée une courbe en.
Courbe gaussienne définition et importance en data science

Définition. La loi normale est une loi de probabilité définie sur les réels définie par 2 paramètres notés μ et σ2. Elle a pour univers l'ensemble des réels. La loi normale de paramètres μ et σ2 est notée. \mathcal {N} (\mu,\sigma^2) N (μ,σ2) Elle est aussi appelée loi de Gauss ou loi de Laplace-Gauss.
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
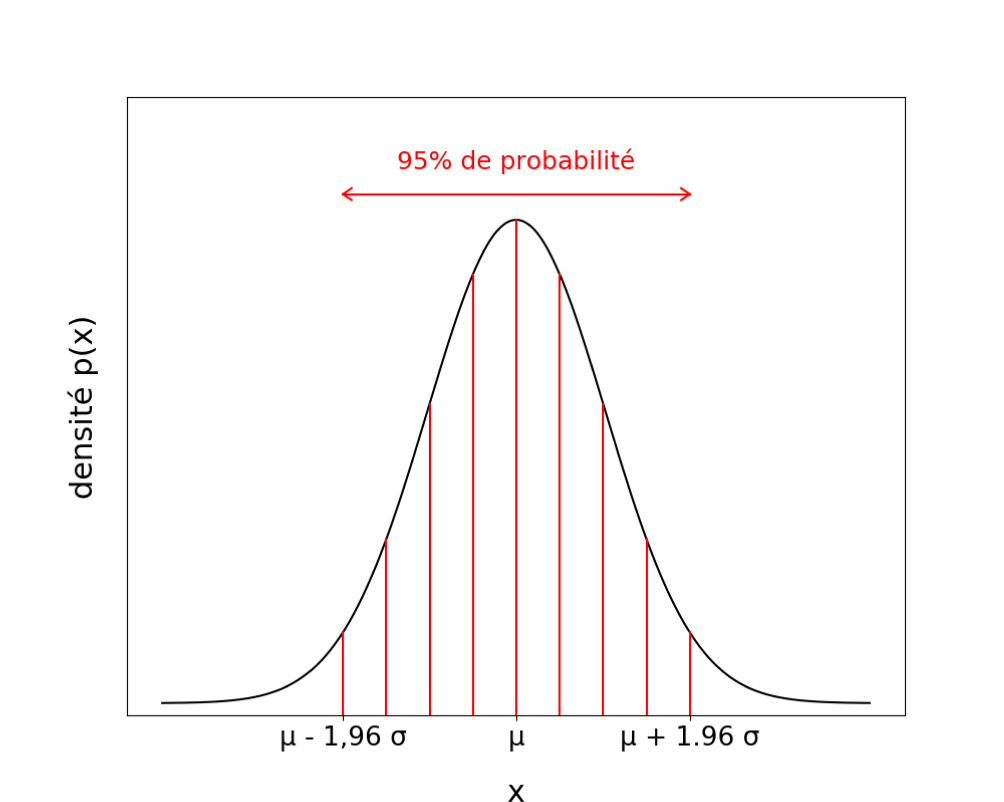
Karl Friedrich Gauss (1777 -1855) : astronome, mathématicien et physicien allemand. Autre nom : courbe en cloche (de Gauss), gaussienne. L'aire entre la courbe et l'asymptote est égale à N ; l'aire de la portion entre m - s et m + s vaut approximativement 2/3 de N ; entre m - 2s et m + 2s elle vaut approximativement 96% de N . Équation.
Distribution normale, aussi distribution gaussienne ou courbe en cloche. Très commun dans la
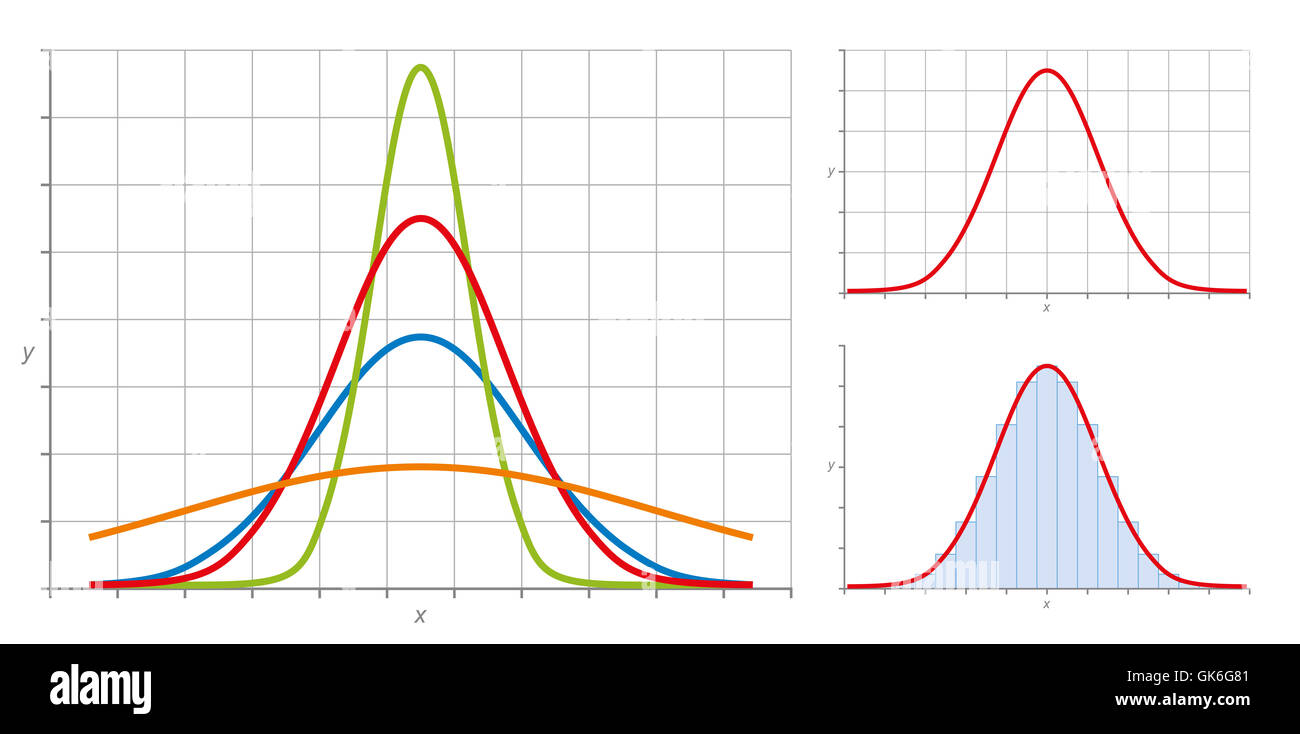
d'inflexion d'abscisses - 1 et 1. LA COURBE DE GAUSS : D'OÙ VIENT-ELLE ? Elle est née au 18e siècle, de la recherche G¶XQH « loi du hasard », et plus précisément du désir de préciser la façon dont la fréquence se rapproche de la probabilité au cours de nombreuses répétitions G¶XQH même épreuve aléatoire. Le but est de.
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
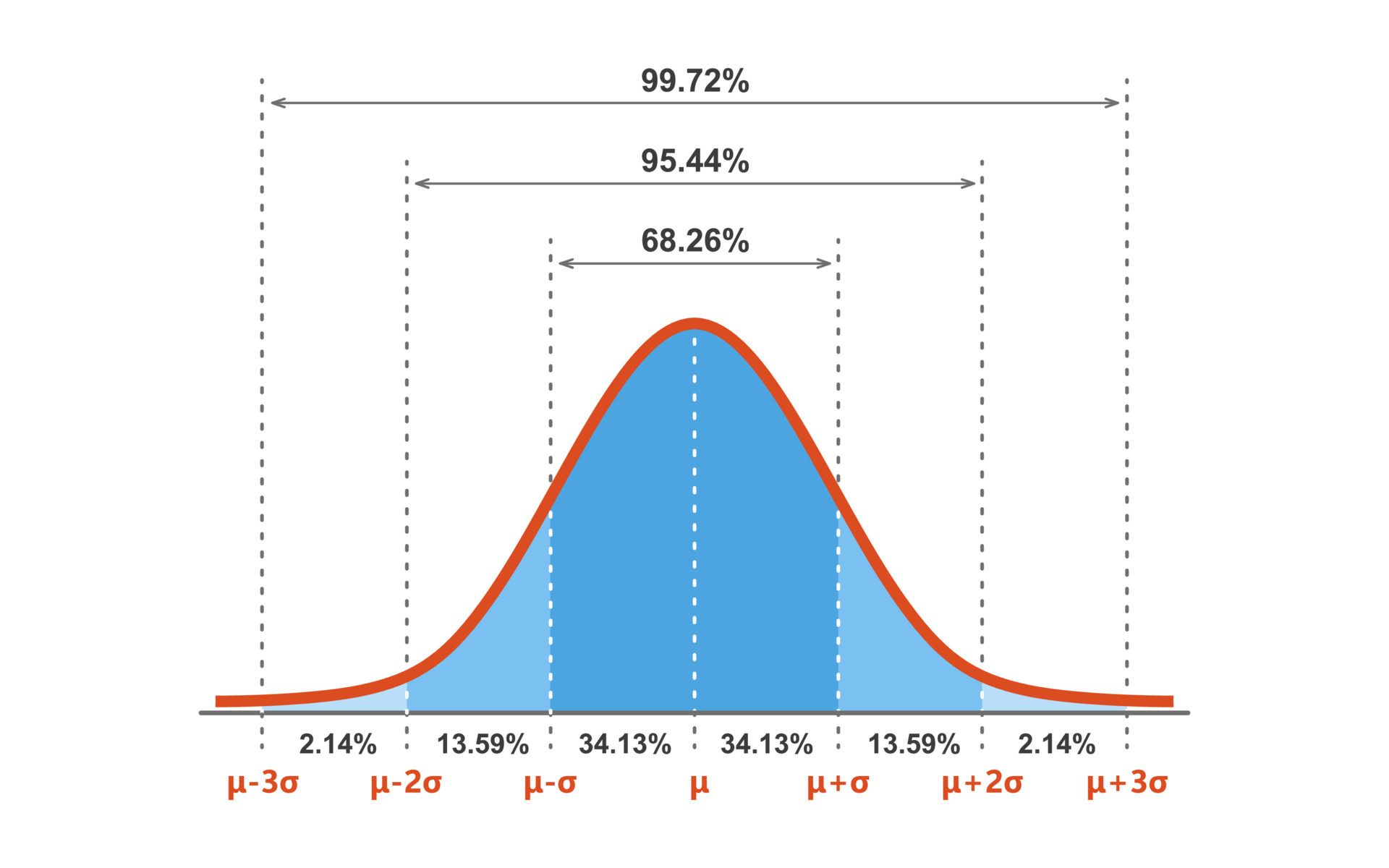
Raphael Kassel. Une courbe gaussienne est une représentation visuelle de données suivant la loi gaussienne. Découvrez la définition complète, et pourquoi cette loi de probabilités est essentielle en Data Science et en Machine Learning. En statistiques, une distribution est une collection de valeurs et de fréquence d'une observation.
Distribution De Gauss Distribution Normale Standard Courbe Graphique En Cloche Gaussienne

La courbe de cette densité est appelée courbe de Gauss ou courbe en cloche, entre autres. C'est la représentation la plus connue de ces lois. C'est la représentation la plus connue de ces lois. Lorsqu'une variable aléatoire X suit une loi normale, elle est dite gaussienne ou normale et il est habituel d'utiliser la notation avec la.
distribución de Gauss. distribución normal estándar. Curva gráfica de campana de Gauss. concepto
Les propriétés d'une distribution normale sont : La fonction de densité de probabilités de la loi normale a la forme d'une courbe en cloche symétrique. la moyenne et la médiane sont égales ; la courbe est centrée sur la moyenne. L'axe des abscisses est une asymptote, σ représente la différence des abscisses entre le sommet de la.
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr 1 LOI NORMALE Le célèbre mathématicien allemand, Carl Friedrich Gauss (1777 ; 1855) conçoit une loi statistique continue, appelée loi normale ou loi de Laplace-Gauss, dont la répartition est représentée par la fameuse courbe en cloche.
3 La Courbe de Gauss (source htt ps // f Download Scientific
Utilisation de la loi normale. Dans notre exemple, nous utiliserons la distribution ci-dessous : La distribution centrée sur 20 et a un écart-type égale à 2. Rappel : Si l'on considère l'aire total sous la courbe elle est égale à 1. La probabilité est directement associée à l'aire et est également égale à 100%.
distribución de Gauss. distribución normal estándar. Curva gráfica de campana de Gauss. concepto
La représentation graphique de cette densité est une courbe en cloche (ou courbe de Gauss). Moments. Les moments de cette loi existent tous. Pour tout , le moment d'ordre n par rapport à l'origine est :. Pour la suite on supposera μ = 0 et σ 2 = 1. En raison de la parité de l' intégrande, tous les moments d'ordre impair sont nuls :
7.6 Distribution Normale Science des données biologiques I
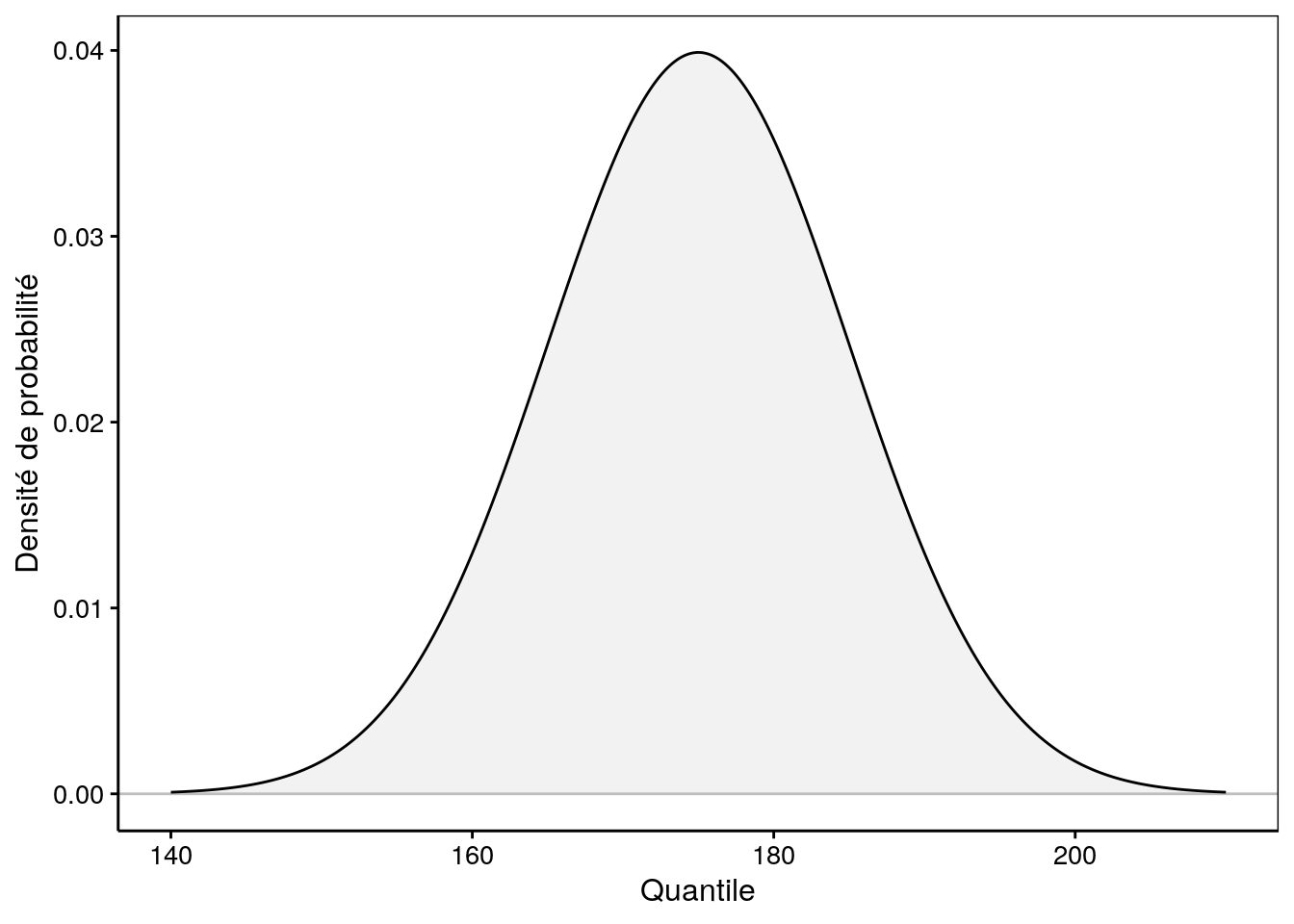
Loi de Laplace-Gauss. Voici la plus connue et la plus utile des lois de probabilité théoriques. Curieusement dénommée loi normale (comme si les autres lois étaient des monstruosités), elle prend aussi le nom du génie Carl Friedrich Gauß (prononcez Gauss).. Mal nommée mais célèbre. Cette loi est la plus célèbre parce qu'elle modélise de nombreuses distributions statistiques.
La Loi normale, loi de Gauss
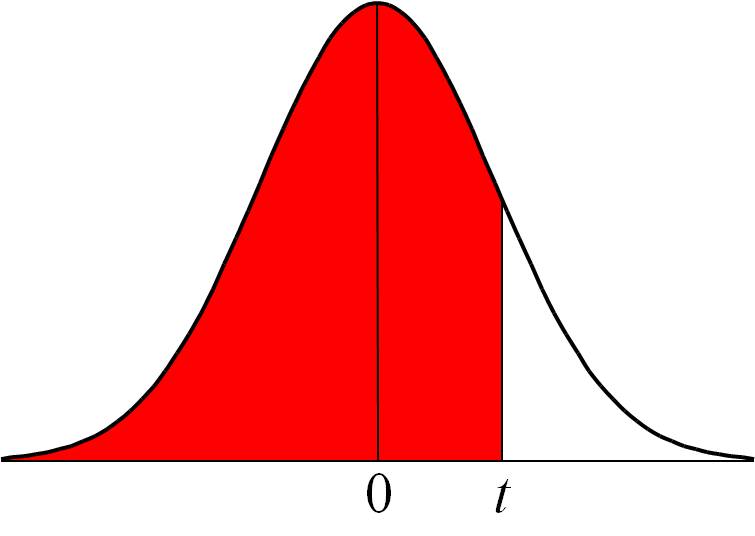
Normal Distribution Overview. The normal distribution, sometimes called the Gaussian distribution, is a two-parameter family of curves. The usual justification for using the normal distribution for modeling is the Central Limit theorem, which states (roughly) that the sum of independent samples from any distribution with finite mean and variance converges to the normal distribution as the.
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
Définition. On appellera distribution gaussienne toute répartition des données dont l'allure a cette forme de « courbe en cloche ». Remarque : Ce type de distribution est classique et se retrouve autant dans des applications de statistiques pures que dans la vie courante : Répartition du nombre d'enfants par famille.
Loi gaussienne Data Analytics Post
Dans un repère orthonormal, la courbe représentative de la fonction est une courbe de Gauss. On dit que c'est une courbe « en cloche », plus ou moins haute ou aplatie selon les paramètres μ et σ. La fonction densité de la loi s'écrit : . Elle n'est pas à connaître en terminale ES. Cela permet d'en tracer quelques.
.